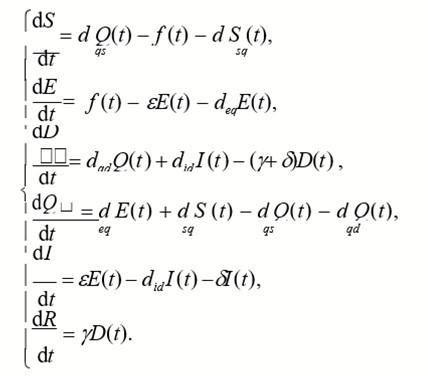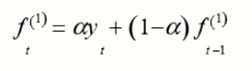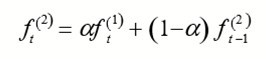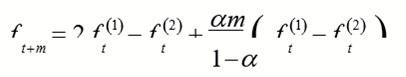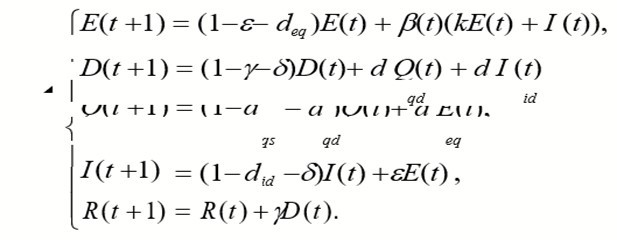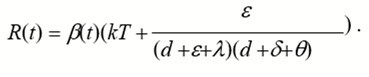Mathematical Modeling and Epidemic Prediction of COVID-19 and its Significance to Epidemic Prevention and Control Measures
Abstract
Background
Since receiving unexplained pneumonia patients at the Jinyintan Hospital in Wuhan, China in December 2019, the new coronavirus (COVID-19) has rapidly spread in Wuhan, China and spread to the entire China and some neighboring countries. We establish the dynamics model of infectious diseases and time series model to predict the trend and short-term prediction of the transmission of COVID-19, which will be conducive to the intervention and prevention of COVID-19 by departments at all levels in mainland China and buy more time for clinical trials.
Methods
Based on the transmission mechanism of COVID-19 in the population and the implemented prevention and control measures, we establish the dynamic models of the six chambers, and establish the time series models based on different mathematical formulas according to the variation law of the original data.
Findings
The results based on time series analysis and kinetic model analysis show that the cumulative diagnosis of pneumonia of COVID-19 in mainland China can reach 36,343 after one week (February 8, 2020), and the number of basic regenerations can reach 4.01. The cumulative number of confirmed diagnoses will reach a peak of 87,701 on March 15, 2020; the number of basic regenerations in Wuhan will reach 4.3, and the cumulative number of confirmed cases in Wuhan will reach peak at 76,982 on March 20. Whether in Mainland China or Wuhan, both the infection rate and the basic regeneration number of COVID-19 continue to decline, and the results of the sensitivity analysis show that the time it takes for a suspected population to be diagnosed as a confirmed population can have a significant impact on the peak size and duration of the cumulative number of diagnoses. Increased mortality leads to additional cases of pneumonia, while increased cure rates are not sensitive to the cumulative number of confirmed cases.
Interpretation
Chinese governments at various levels have intervened in many ways to control the epidemic. According to the results of the model analysis, we believe that the emergency intervention measures adopted in the early stage of the epidemic, such as blocking Wuhan, restricting the flow of people in Hubei province, and increasing the support to Wuhan, had a crucial restraining effect on the original spread of the epidemic.
It is a very effective prevention and treatment method to continue to increase investment in various medical resources to ensure that suspected patients can be diagnosed and treated in a timely manner.
Based on the results of the sensitivity analysis, we believe that enhanced treatment of the bodies of deceased patients can be effective in ensuring that the bodies themselves and the process do not result in additional viral infections, and once the pneumonia patients with the COVID-19 are cured, the antibodies left in their bodies may prevent them from reinfection COVID-19 for a longer period of time.
Author Contributions
Academic Editor: Reza Razaghi, School of Mechanical Engineering, Iran University of Science & Technology, Narmak, Tehran, Iran.
Checked for plagiarism: Yes
Review by: Single-blind
Copyright 2020 Yichi Li, et al.
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
Since December 2019, many unexplained cases of pneumonia with cough, dyspnea, fatigue, and fever as the main symptoms have occurred in Wuhan, China in a short period of time. 1, 2
China's health authorities and CDC quickly identified the pathogen of such cases as a new type of coronavirus, which the World Health Organization (WHO) named COVID-19 on January 10, 2020. 3
On January 22, 2020, the Information Office of the State Council of the People's Republic of China held a press conference introduced the relevant situation of pneumonia prevention and control of new coronavirus infection.
On the same day, the People's Republic of China's CDC released a plan for the prevention and control of pneumonitis of new coronavirus infection, including the COVID-19 epidemic Research, specimen collection and testing, tracking and management of close contacts, and propaganda, education and risk communication to the public. 4
Wuhan, China is the origin of COVID-19 and one of the cities most affected by it. The Mayor of Wuhan stated at a press conference on January 31, 2020 that Wuhan is urgently building Vulcan Mountain Hospital and Thunder Mountain Hospital patients will be officially admitted on February 3 and February 6. 5 By 24:00 on February 6, 2020, a total of 31,161 confirmed cases, including 636 deaths, were reported in the Chinese mainland, 22,112 confirmed cases, including 618 deaths, were reported in Hubei province, and 11,618 confirmed cases, including 478 deaths, were reported in Wuhan city. The spread of COVID-19 and various interventions have had an incalculable negative impact on People's daily lives and the normal functioning of society. Cities in China's Hubei province have issued varying degrees of closures and traffic restrictions. 6
In fact, there are many imminent questions about the spread of COVID-19. How many people will be infected tomorrow? When will the inflection point of the infection rate appear? How many people will be infected during the peak period? Can existing interventions effectively control the COVID-19? What mathematical models are available to help us answer these questions?
The COVID-19 is a novel coronavirus that was only discovered in December 2019, so data on the outbreak is still insufficient, and medical means such as clinical trials are still in a difficult exploratory stage. 7 So far, epidemic data have been difficult to apply directly to existing mathematical models, and questions need to be addressed as to how effective the existing emergency response has been and how to invest medical resources more scientifically in the future and so on. Based on this, this article aims to study the gaps in this part.
Methods
Data
Recently, COVID-19 suddenly struck in Wuhan, the seventh largest city of the People's Republic of China. The daily epidemic announcement provides us with basic data of epidemiological research. We obtained the epidemic data from the National Health Commission of the People's Republic of China from January 10, 2020 to February 9, 2020, including the cumulative number of cases, the cumulative number of suspected cases, the cumulative number of people in recovery, the cumulative number of deaths and the cumulative number of people in quarantine in the Chinese mainland. 8 At the same time, we collected the epidemic data of Hubei Province and its capital city Wuhan from the Health Commission of a Province from January 20, 2020 to February 2, 2020, including the cumulative number of cases, the cumulative number of recovered people and the cumulative number of quarantined people in Hubei Province and Wuhan. 9
The Model
Based on the collected epidemic data, we tried to find the propagation rule of the COVID-19, predict the epidemic situation, and then propose effective control and prevention methods. There are generally three kinds of methods to study the law of infectious disease transmission. The first is to establish a dynamic model of infectious diseases; The second is statistical modeling based on random process, time series analysis and other statistical methods. The third is to use data mining technology to obtain the information in the data and find the epidemic law of infectious diseases. 10 Considering the shortage of the collected public data in time span, the research content of this paper is mainly based on the first two kinds of methods. The spread of the COVID-19 has exploded rapidly in Wuhan, China, and effective government intervention and prevention and control measures in all sectors depend on the best possible outbreak prediction. 11 This paper mainly builds a dynamic model of COVID-19 transmission and a statistical model based on time series analysis, and compares the prediction effects of these mathematical models on the spread of COVID-19 epidemic. Due to the outbreak of existing data is not relatively large sample data, in the spread of COVID-19 at this stage, the dynamics model we built is more suitable for containing parameters to be estimated to predict the development trend of epidemic, peak size, etc., based on time series analysis of statistical modeling is more accurately predict the value of data in the short term.
SEIQDR-Based Method for Estimation
After the outbreak of the COVID-19 epidemic, the Chinese government has taken many effective measures to combat the epidemic, such as inspection detention, isolation treatment, isolation of cities, and stopping traffic on main roads. 12, 13, 14 However, the traditional SEIR model cannot fully describe the impact of these measures on different populations. Based on the analysis of the actual situation and existing data, we divided the population into different warehouses and established a more effective model for the dynamic spread of infectious diseases. According to the actual situation of the epidemic, we divided the population into 6 different categories to comply with the current spread of COVID-19 in China. Seeing Table 1 for specific classification.
Table 1. Classification and definition of population under transmission of new coronavirus.| Classes | Explanations for different classes |
| S(t) | People who may be infected by the virus |
| E(t) | Infected with the virus but without the typical symptoms of infection |
| I(t) | Infected with the virus and highly infectious but not quarantined |
| Q(t) | Diagnosed and quarantined |
| D(t) | Suspected cases of infection or potential victims |
| R(t) | People who are cured after infection |
Since the incubation period of the COVID-19 is as long as 2 to 14 days, there are already infected but undetected people (E) in the natural environment of the susceptible population (S), when the first case is identified. Some people who have been infected need to go through a certain incubation period before suspected symptoms can be detected (Q). Chest CT imaging was used to observe whether there were glassy shadows in the lungs to determine whether the diagnosis was confirmed (D). Another part of the population has been infected and has been sick, because not isolated, is highly infectious in the population. After a period of quarantine treatment, these two groups of people will be discharged from hospital (R), or face death due to basic diseases, based on these, we classify the population as shown in Table 1.
As shown in Figure 1, we set up the warehouse in this way to help us build a clear and accurate COVID-19 transmission dynamics model. The diagnosed patients will become healed after a certain period of isolation and treatment. We call the proportion of people who are cured per day to those who are diagnosed the cure rate γ, which reflects the local level of care and, to another extent, the difficulty of the condition. And is the fatality rate of the new pneumonia, reflecting the lethal intensity of COVID-19. The rate dqd at which suspected patients are converted into confirmed cases represents a measure of quarantine intensity due to the constant changes in medical procedures. At the same time, some highly infectious people in the free environment will be transferred to confirmed cases at the rate of did, while others will be moved out at the rate of due to lack of timely treatment.
Figure 1.Warehouse transfer diagram of SEIQDR Model.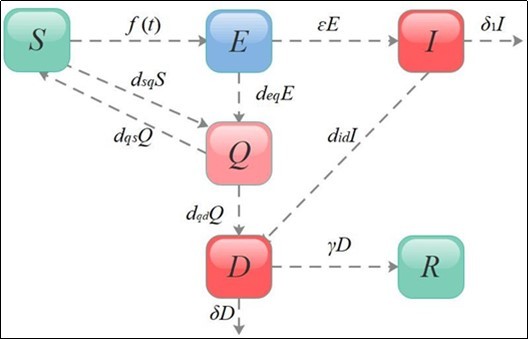
The incidence rate of the susceptible population S(t) was set as f(t), which to some extent can reflect the infection degree of COVID-19 in the susceptible population. The susceptible population in the free environment will become latent after being infected by COVID-19, and gradually develop after the incubation period. The proportion of latent persons who were converted to free infection was e, and the proportion identified as suspected cases was deq. After medical diagnosis, some of the suspected cases were confirmed, while others were not detected and returned to the susceptible population with a ratio of dqs. The susceptible population has also been converted to suspected cases at a rate of dqs. According to the above-mentioned population classification and parameter definitions, we have established a SEDQIR model based on SEIR, which can better reflect the spread of the COVID-19 in the population. 18 The SEDQIR model established based on the dynamic transmission mechanism of infectious diseases is as follows:
In order to study the deeper COVID-19 transmission rule, we perform a detailed analysis of some parameters to transform the degree of infection into a form more conducive to data expression. 19Adopt the degree of infection of COVID-19 in susceptible populations f (t ) , the mathematical expression is as follows:
Among them, we refer to the infection rate coefficients of latent and freely infected people in susceptible populations as βE and βI. At this stage, the epidemic caused by COVID-19 may still be in the early stages of spreading among the population. We need to fit and estimate the above parameters through the original data published by the National Health Commission of China. Therefore, we will formulate the formula to a certain extent. Simplify: f(t) = β(t)(kE + I)
The infection rate β(t) can be estimated and fitted based on the existing data, and k value reflects the infectivity of the latent person relative to the infected person. Furthermore, according to the definition of incidence, the rate of infection can be expressed by the number of people diagnosed over a period of time. 10 If the number of people diagnosed on day t is F, the infection rate can be expressed as
Among them, d1 is the average incubation period of COVID-19, and d2 is the time during which the incubator is isolated after the incubation period. Based on the available data, the infectious rate can be calculated numerically.
TS Model-Based Method for Estimation
Both the exponential smoothing method and the ARIMAX model are time series analysis methods, and these methods are often used in statistical modeling to analyze changes that occur over time. 20, 21 In order to accurately predict the number of confirmed cases, cumulative rehabilitation and cumulative deaths of COVID- 19 in mainland China and Hubei Province in the future, We have established multiple time series analysis models based on different mathematical formulas and tested the statistics of these time series models, and compare the results with the predicted effect.
The spread of COVID-19 in the population has not been more than two months. Based on statistical modeling methods, we still cannot know the seasonal fluctuations of COVID-19. Through simple data observation, we find that the spread of COVID-19 in the population may have some trends, so when we tried to use the exponential smoothing-based time series prediction, we used the Brown linear exponential smoothing model to analyze the relevant data of COVID-19. Compared with the primary exponential smoothing model, the Brown linear exponential smoothing model contains two Term exponential smoothing value. 22 The linear exponential smoothing formula using Brown's linear exponential smoothing model is as follows:
Brown's linear exponential smoothing formula is as follows:
Among them, ft (1) is the exponential smoothing value of the model, ft (2) is the quadratic exponential smoothing value of the model. 23 The Brown linear exponential smoothing model using these two smoothed values is as follows:
In the above formula, m is the number of lead periods.
Time series analysis based on exponential smoothing is a statistical modeling method that cannot consider input variables. Considering that the COVID-19 confirmed cases, cumulative deaths, and cumulative recovery variables may have some relationship in value, the time series analysis based on ARIMAX models will also be performed on these variables in Mainland China, Hubei Province, Wuhan City and some surrounding cities, and these time series models will be compared and selected according to the test and prediction effects of statistics.24 In order to make accurate prediction of 2019 nCoV in the population, the formula of ARIMAX model is as follows
The ARIMAX model can be seen as an ARIMA model with an intervention sequence. Taking the number of confirmed cases that we are most concerned about when COVID-19 spreads through the population as an example, the model can represent the sequence value of the number of confirmed cases over a period of time as random fluctuations the past value of the number of confirmed cases and the past value of the input sequence, the input sequence may be variables that have a high degree of correlation with the number of confirmed cases, such as the number of deaths, the cumulative number of recoveries, and the number of suspected cases.
Simulation
Due to the long duration of the COVID-19 epidemic, it is still in an ascending period as of February 9. In this paper, days are taken as the minimum time unit, a discrete model is obtained according to the practical meaning of the continuous model, and the epidemic data of Hubei province and the whole country are used to obtain the changes of its parameters, and the numerical simulation is carried out. If the number of days is taken as the minimum time unit, the continuous model can be discretized as:
According to the discrete model, the initial value of each variable can be given to describe the model numerically when the parameters are determined. We give the initial values of some parameters according to the references and the latest outbreak information, and we will use the least square method to obtain the variables and parameters that cannot be determined. According to the literature 1, 15, 16, 17, the average incubation period of COVID-19 is 7 days, and the average onset period is 1 day after the incubation period. The average disease duration is 21 days, and the mortality rate based on historical data, it is about 2%. The daily conversion of suspected cases to confirmed cases accounts for about 0.8, and newly admitted patients account for about 0.2 confirmed cases per day. 25 Therefore, the following parameters can be preliminary estimated, these parameters reflect the basic situation of the epidemic at this stage.
In this paper, the least square method is used to fit the unknown parameters, but the value of k and the infection rate of b(t) in the model are still unknown. According to the number of confirmed cases published by the national health and fitness commission of China and Hubei provincial health and fitness commission, we calculated the discrete value of the infection rate on January 20 solstice and February 5, and obtained the parameter k by using the least square method. Finally, we obtained the numerical solution of the model, so as to conduct a more detailed model analysis. 27, 28 Let the calculated number of diagnosed persons with parameters be calculated as Dc . When the actual number of confirmed patients is D , we construct a least squares estimate method to fit the parameters. The calculation formula of the error SSE is as follows:
Results
TS Model-Based Estimates
We use sequence diagrams and autocorrelation functions of the original data to determine the stationarity of these time series, and to smooth the series whose average and variance are not always constant. In the exponential smoothing method, we perform a natural logarithmic transformation on the series to omplete the smoothing process. In the ARIMA and ARIMAX models, we use the first-order difference or the second- order difference to smooth the original sequence. Using the above processing, we can obtain the time series analysis model summary information of the number of confirmed cases in mainland China as shown in Table 2.
Table 2. Summary of 6 time series models of cumulative confirmed cases in mainland China.| Method | Stability treatment | Model | Fitting effect | Ljung- Box Q(18) | Number of Outliers | Serial number | ||
| Stationary R-squared | R-squared | Normalized BIC | Sig. | |||||
| Exponential smoothing method | _ | Brown | 0.245 | 0.996 | 11.338 | 0.787 | 0 | 1 |
| Natural logarithmic transformation | Brown | 0.605 | 0.992 | 12.039 | 0.958 | 0 | 2 | |
| ARIMA | First order difference | ARIMA (0,1,0) | 0.235 | 0.961 | 13.644 | 0.000 | 0 | 3 |
| Two order difference | ARIMA (0,2,0) | 0.687 | 0.997 | 11.223 | 0.912 | 0 | 4 | |
| ARIMAX | First order difference | ARIMA X(0,1,0) | 0.977 | 0.999 | 10.634 | 0.987 | 0 | 5 |
| Two order difference | ARIMA X(0,2,0) | 0.208 | 0.997 | 11.793 | 0.997 | 0 | 6 | |
As shown in Table 2, we have established multiple time series analysis models for the number of confirmed cases in mainland China. By comparing, we can initially find that the Brown model is a natural logarithmic transformation of the original sequence and the second order ARIMAX (0,1,0) model for difference processing seems to be more suitable. Among them, the Brown model has a stationary R-square of 0.605, the Ljung-Box Q (18) test statistic has a value of 0.958, the stationary R-square of the ARIMAX (0,1,0) model is 0.977, and the value of the Ljung-Box Q (18) test statistic is 0.987. According to Table 2, we find that ARIMAX (0,1,0) model is the best of the six time series models in terms of goodness of fit and Ljung box Q (18) test results. We preliminarily think that Brown model and ARIMAX (0,1,0) model should have good statistical significance, and they should be able to predict the number of confirmed cases of new coronavirus pneumonia in mainland China in the next week. To further diagnose the results of these time series models, we make their autocorrelation function diagrams of the residuals as shown in Figure 2.
Figure 2.Residual ACF of six time series models of cumulative confirmed cases in mainland China.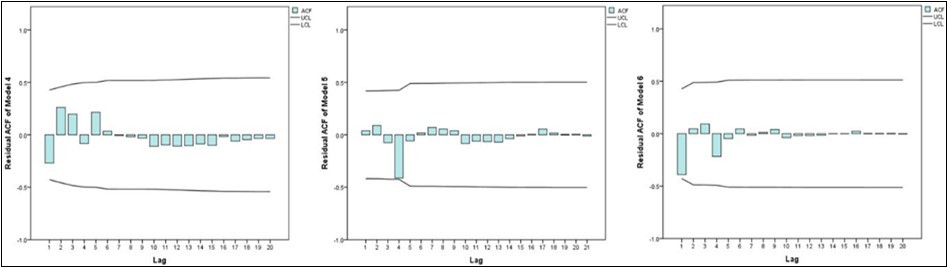
In the function graph, we can judge whether the residuals still contain valid information of the time series. Through Figure 2, we can intuitively find that there may still be some valid information in the residuals of model 3. After observing the Residual ACF of other models, we think the residual sequences of Model 2 and Model 5 can be regarded as white noise sequences.29 That is, to a certain extent, the Brown model with natural logarithmic transformation of the original sequence and ARIMAX (0,1,0) models can be used to predict the short-term development of the confirmed number of patients with new type of coronavirus pneumonia in mainland China. As shown in Figure 3 and Figure 4 below, we have made a short-term prediction of the number of confirmed cases of new coronavirus pneumonia in mainland China based on Brown model and ARIMAX (0,1,0) model after second-order difference processing. We can clearly see from Figure 3 and Figure 4 that the prediction of the exact number of cases diagnosed in the past time by these two models is in good agreement with the real value, while the ARIMAX (0,1,0) model processed by second-order difference is more consistent with the historical data. The predictions of these two models for the number of confirmed cases of new coronavirus pneumonia in the next week are relatively close, but we noticed that under the 95% confidence interval, the ARIMAX (0,1,0) after second-order difference processing the upper and lower limits of the model's prediction of the number of confirmed cases are very small, so we finally selected the ARIMAX (0,1,0) model that was subjected to second-order difference processing in six time series models.
Figure 3.Prediction chart of cumulative number of confirmed cases in mainland China based on logarithm transformation Brown model.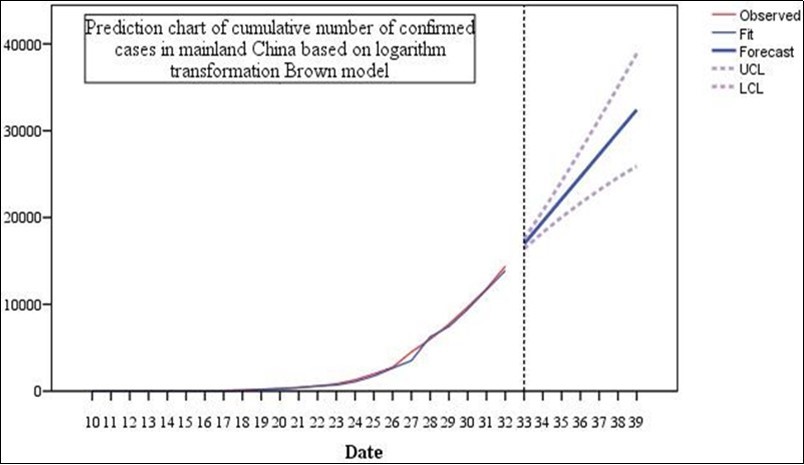
Figure 4.Prediction chart of cumulative number of confirmed cases in mainland China based on ARIMAX(0,1,0).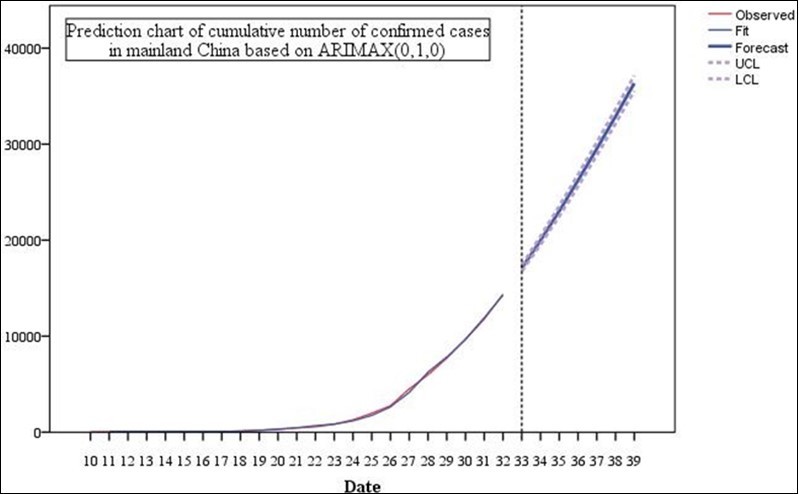
Then the number of confirmed cases in mainland China is predicted. Based on the predictions in Figure 4, we believe that the number of confirmed cases of new coronavirus pneumonia in mainland China in a week (February 8, 2020) may be as high as 36,343.
We also made six time series models of cumulative confirmed cases in Hubei Province as shown in Table 3 below and the autocorrelation function diagrams of the residuals of these 6 models are shown in Figure 5. Based on the information in Table 3 and Figure 5, we selected the ARIMAX (0,0,0) model made a short- term prediction of the number of confirmed cases of pneumonitis of the new coronavirus in Hubei Province, and plotted the prediction of the ARIMAX (0,0,0) model as shown in Figure 6.
Table 3. Summary of 6 time series models of cumulative confirmed cases in Hubei Province.| Method | Stability treatment | Model | Fitting effect | Ljung- Box Q(18) | Number of Outliers | Serial number | ||
| Stationary R-squared | R-squared | Normalized BIC | Sig. | |||||
| Exponential smoothing method | _ | Brown | 0.136 | 0.994 | 11.228 | 0.958 | 0 | 7 |
| Natural logarithmic transformation | Brown | 0.021 | 0.987 | 11.928 | 0.845 | 0 | 8 | |
| ARIMA | First order difference | ARIMA (0,1,0) | 0.205 | 0.958 | 13.141 | 0.000 | 0 | 9 |
| Two order difference | ARIMA (0,2,0) | 0.264 | 0.994 | 11.200 | 0.977 | 0 | 10 | |
| ARIMAX | _ | ARIMA X(0,0,0) | 0.999 | 0.999 | 10.383 | 0.806 | 0 | 11 |
| First order difference | ARIMA X(0,1,0) | 0.973 | 0.999 | 10.279 | 0.655 | 0 | 12 | |
Figure 5.Residual ACF of six time series models of cumulative confirmed cases in Hubei Province.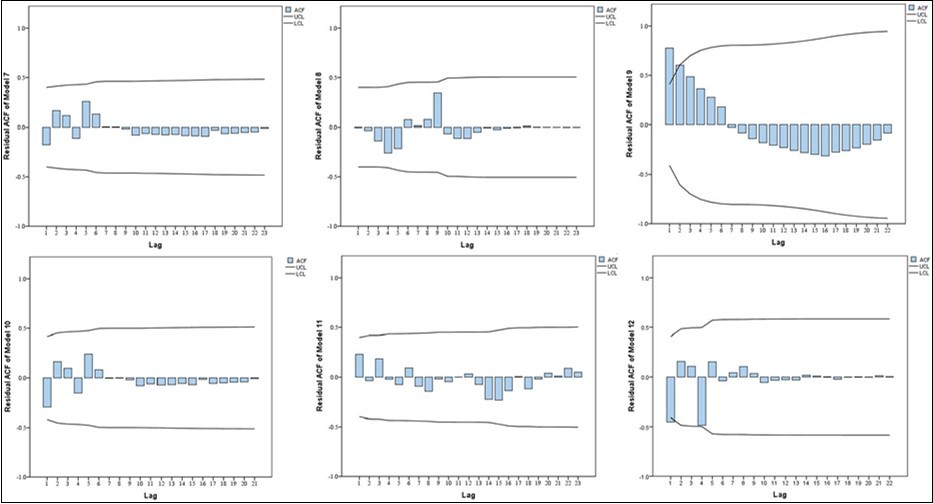
Figure 6.Prediction chart of cumulative number of confirmed cases in Hubei Province Based on ARIMAX(0,0,0).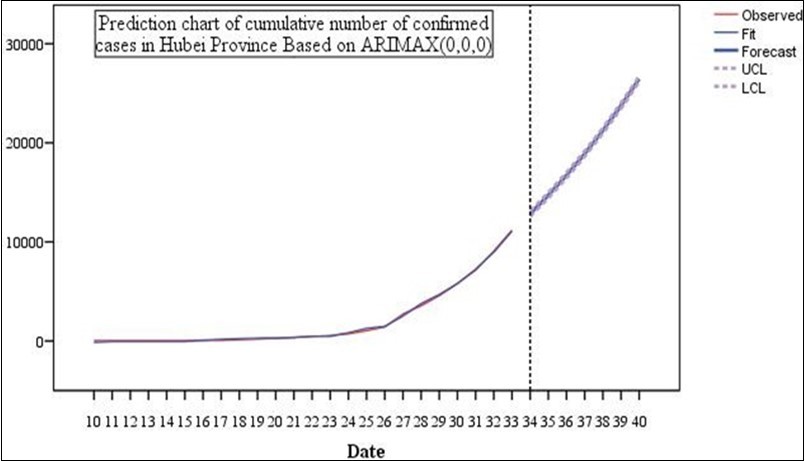
According to Figure 6, we believe that the number of confirmed cases of pneumonitis with new coronavirus in Hubei Province will rise to 26,455 in a week (February 8, 2020). It is worth mentioning that because the time series model is based on the original sequence itself time series models based on different mathematical formulas may not be suitable for long-term prediction of the spread of the COVID-19 epidemic, but these models can provide rapid prediction of short-term transmission of the COVID-19 epidemic. So as to provide reference value for all levels of departments and hospitals in the next few days to implement effective intervention and prevention of the spread of new coronavirus.
SEIQDR-Based Estimates
According to the data released by the National Health Construction Commission of China, we set the data on January 10 as the initial value. On January 10, the transmission of COVID-19 only occurred in Hubei Province, of which 41 were confirmed, 0 were suspected, 2 were cured, 2 were infected with the COVID-19 but not yet sick, and 0 people were ill but not isolated, namely:
E(0) = 2 , I (0) = 0 , Q(0) = 0 , D(0) = 41 , R(0) = 2 .
Since COVID-19 originates from Wuhan, Hubei, the above initial value can also be used as the national initial value. Based on this, we use the least square method to calculate k and errors SSE of Hubei Province and Mainland China as follows:
kH= 0.815 , SSEH= 2236 .
kN= 0.553 , SSEN= 2527 .
Among them, kH means Hubei Province’s k value, kN means the k value of mainland China, because Hubei Province is the birthplace of the epidemic, with a large number of patients and limited medical resources, a large number of mild patients are self-isolated at home, which increases the transmission time after the incubation period. 30 The number of cases outside Hubei Province is small, and medical resources are sufficient, making the k value small. The latent can get timely treatment after the onset, and reduce the transmission time after the onset. It can be seen from the comparison of k value that it is a very correct and effective decision for medical staff from other provinces in mainland China to go to Wuhan and Hubei to fight the epidemic. It can be seen from Figure 7 that the SEIQDR model based on the dynamic propagation of COVID-19 has a good fitting effect with the original data in the duration period (from January 10, 2020 to February 9, 2020), and the fitting curve of the number of confirmed cases is basically consistent with the duration data.
Figure 7.Matching effect chart of the real value and predicted value of the cumulative number of confirmed cases in China and Wuhan.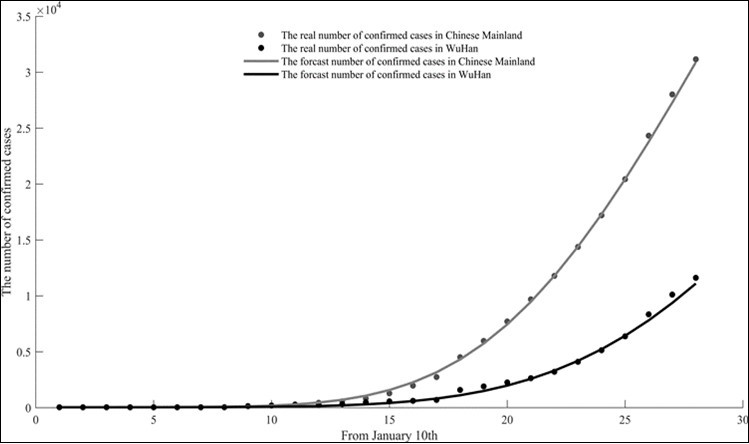
We use SEIQDR model to predict the spread of COVID-19 in mainland China and Wuhan, and get the development trend of the cumulative number of confirmed cases in mainland China and Wuhan as shown in Figure 8. Based on the prediction results in Figure 8, we believe that the cumulative number of confirmed cases in Wuhan will continue to rise within 70 days from January 10, 2020, and the cumulative number of confirmed cases in Wuhan may reach a peak around March 20, 2020, the peak is 76982, that is to say, after the cumulative number of confirmed cases in Wuhan reached 76982 on March 20, there may no new confirmed cases appear.
Figure 8.Prediction results of cumulative number of confirmed cases in China and Wuhan.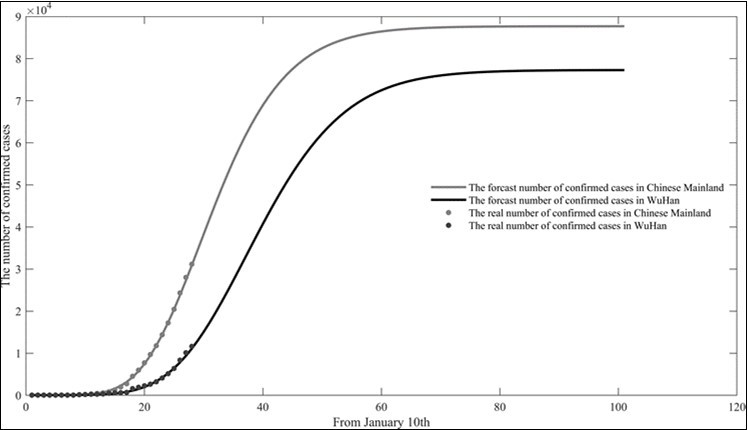
To observe the development trend of the cumulative number of confirmed cases in mainland China, we believe that when the cumulative number of confirmed cases in Wuhan reaches a peak, the growth rate of confirmed cases in mainland China will decrease rapidly, and the cumulative number of confirmed cases in mainland China will peak around March 15, 2020, with a peak of 87,701. In order to give a clearer mathematical description of the spread of COVID-19 in Wuhan and Mainland China, we analyze the infection rate and basic regeneration number of the new coronavirus. Using the diachronic data and the calculation formula for the infection rate given above, the infection rate is fitted, we let the basic regeneration number of COVID-19 be R(t) , we use the following formula to calculate the basic regeneration number of COVID-19:
As can be seen from the above formula, there is a close relationship between the basic regeneration number and the infection rate. In the above formula, t is the average latency of the COVID-19, and we also set the initial value of the average latency to 7. From this, we can get the trend of infection rate and basic regeneration number of 2019 nCoV in Wuhan and Mainland China over time as shown in Figure 9 below. As shown in Figure 9, during the period from January 10 to February 9, 2020, No matter in mainland China or Wuhan, the infection rate and basic regeneration number of COVID-19 continue to decline, and may continue to decline in the future. In our opinion, this may indicate that the emergency intervention and special control measures taken by the Chinese government to block Wuhan City, restrict the flow of people in Hubei Province and enhance the medical resources in the severely affected areas in the early stage of COVID-19 transmission have played a crucial role in the spread of the epidemic. According to the results of SEIQDR model, we believe that during the period from January 10 to February 9, 2020, the average basic regeneration number of COVID-19 in mainland China is 4.01, while the average basic regeneration number in Wuhan is 4.3. The infection rate of COVID-19 in mainland China should be reduced to 0 in 45 days after January 10, 2020, that is, around February 25.
Figure 9.Infection rate band basic regeneration number R0 in China and Wuhan.
According to the results of the SEIQDR model, we can also study more about the development trend of the COVID-19 epidemic in mainland China, Hubei Province, and Wuhan. Without the loss of generality, other parameters in the SEIQDR model remain initially set. Under the circumstances, we analyze some parameters in mainland China to explore the possible changes in the cumulative number of confirmed diagnoses. We have made a trend chart of the number of confirmed cases in mainland China when the average time required for the suspected population to be transformed into the confirmed population changes as shown in Figure 10.
Figure 10.The changes of different in the cumulative of confirmed cases in mainland China during the COVID-19 transmission process.
In Figure 10, The reciprocal of s indicates that it takes the average time for the suspected population to be diagnosed as the confirmed population, that is = dqd , as shown in Figure 10, at that time of = 1 / 5 , it took an average of 5 days for suspected cases to be diagnosed as confirmed cases for necessary isolation and treatment. If the various preventive measures remain unchanged, the cumulative number of confirmed patients in mainland China will reach a peak after 73 days on January 1, 2020. The peak time was 94731 people. At that time of = 1 / 3 , patients can get relatively timely isolation and treatment after the onset of the disease, in which case the peak number of cumulative diagnoses will be reduced to 87701, a relative decrease of 7030. According to Figure 10, we can find that the peak number increases as gets smaller of cumulative diagnoses, which means that if the number of patients diagnosed with suspected patients will increase rapidly if they are not diagnosed in time. We believe that this trend may not be obvious enough within 30 days after January 10, however, once the epidemic situation becomes serious, the rapid increase in the number of confirmed cases and the difficulty in timely diagnosis and treatment may bring great challenges to the prevention and control of the epidemic in mainland China.
Finally, we analyzed the sensitivity of mortality and cure rate in SEIQDR model. The Figure 11 shows the change in the cumulative number of confirmed cases with mortality and cure rate in mainland China. In Figure 11, on the left is the cumulative number of confirmed diagnoses with death during the transmission of COVID-19 in mainland China, the change of the cure rate is the change of the cumulative number of diagnoses with the cure rate on the right.
Figure 11.Sensitivity analysis results of mortality and cure rate.
We found that when the mortality rate gradually increased from 2% to 10%, the cumulative number of diagnoses increased by about 2,000. We believe that ,this means that the bodies of patients killed by COVID 19 may still carry a certain number of new infectious coronaviruses. According to the results of this simulation, we suggest that mainland China, especially Hubei Province and Wuhan City, should pay attention to the treatment of the dead bodies of the dead patients, try to ensure that the body itself and the handling process do not cause additional contagion. We also gradually increased the cure rate from 2% to 10%, and found that the cumulative number of confirmed diagnoses has almost no fluctuation. We think this means that once the pneumonia patients with the new coronavirus are cured, the antibodies left in their bodies may make them no longer a member of the susceptible population infected with the new coronavirus. In the early stage of COVID-19 transmission, as we did not know about COVID-19 and clinical trials were difficult to proceed immediately, our modeling and results provided reference values for intervention and prevention and clinical trials at all levels.
Discussion
There is no doubt that the propagation of COVID-19 in the population will be affected by the intricacies of many factors. In the early stage of the COVID-19 propagation, it is difficult to establish a dynamic propagation model with parameters to be estimated and obtain fairly accurate simulation results, but the preliminary estimation of parameters such as average latency and mortality through existing data may be helpful for solving important parameters such as infection rate and rehabilitation rate, which will help us have a more accurate grasp of the transmission trend of COVID-19. On the other hand, statistical modeling of the spread of new coronavirus pneumonia in the population based on time series analysis is a thing that can be done immediately after getting the latest data every day, because the dynamic model of the time series is based on the law of the data itself. Although this method often requires sufficient data to support it, in the early stages of epidemic transmission, this method can still be used to more accurately predict the indicators of epidemic transmission in the short term, so as to provide intervention control at all levels of the departments and Policy implementation provides short-term emergency prevention programs.
Limitations
This article will inevitably make some assumptions when building the model. When we build a dynamic discrete model for a certain period of time for COVID-19, we ignore the impact of factors such as population birth rate and natural mortality.
For simple calculations, we also Assume that the latent population of COVID-19 and the infected but not yet isolated population have the same range of activities and capabilities, that is, we assume that for COVID-19, the population E(t) And the crowd I(t) have the same contact rate. On the other hand, this article is based on the collected data for a specific period of time to fit and estimate the basic regeneration number, infection rate, and recovery rate of COVID-19, with the continuous release of epidemic data these important indicators may undergo significant changes in the spread of COVID-19 among the population.
Acknowledgements
This work was supported by the Philosophical and Social Sciences Research Project of Hubei Education Department (19Y049), and the Staring Research Foundation for the Ph.D. of Hubei University of Technology (BSQD2019054), Hubei Province, China.
References
- 1.Huang C, Wang Y, Li X. (2020) Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China[J]. The Lancet.
- 2.Shen M, Peng Z, Xiao Y. (2020) Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China[J]. bioRxiv.
- 3. (2020) World Health Organization (WHO). , Coronavirus.https://www.who.int/health-topics/coronavirus[Accessed 08.
- 4. (2020) . National Health Commission of the People’s Republic of China.http://www.nhc.gov.cn/xwzb/webcontroller.do?titleSeq=11208&gecstype=1[Accessed 08 .
- 5. (2020) . Health Commission of Hubei Province.http://wjw.Hubei.gov.cn/bmdt/ztzl/fkxxgzbdgrfyyq/fkdt/202002/t20200201_2017239.shtml[Accessed 08 .
- 6. (2020) . Health Commission of Hubei Province.http://wjw.Hubei.gov.cn/bmdt/ztzl/fkxxgzbdgrfyyq/fkdt/202001/t20200123_2014470.shtml[Accessed 08 .
- 7.Chan J F W, Yuan S, K H. (2020) A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster[J]. The Lancet.
- 8. (2020) . , National Health Commission of the People’s Republic of China.http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml[Accessed 08.
- 9. (2020) . , Health Commission of Hubei Province.http://wjw.Hubei.gov.cn/bmdt/ztzl/fkxxgzbdgrfyyq/xxfb/[Accessed 08.
- 10.Z E Ma, Y C Zhou, W D. (2004) Mathematical modeling and research of infectious disease dynamics [J].
- 11.Wu P, Hao X, Lau E H Y. (2020) Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan. , China, [J], Eurosurveillance 25(3).
- 12. (2020) . National Health Commission of the People’s Republic of China.http://www.nhc.gov.cn/xcs/ptpxw/202001/8005b53f000f4f1185ec0175d6543fbf.shtml[Accessed 08 .
- 13. (2020) . National Health Commission of the People’s Republic of China.http://www.nhc.gov.cn/xcs/fkdt/202001/de4be3098142493bb8a3de170662857a.shtml[Accessed 07 .
- 14. (2020) . Health Commission of Hubei Province.http://wjw.Hubei.gov.cn/bmdt/ztzl/fkxxgzbdgrfyyq/fkdt/202002/t20200207_2021083.shtml[Accessed 08 .
- 15.J M Read, Bridgen J R E, Cummings D A T. (2020) Novel coronavirus COVID-19: early estimation of epidemiological parameters and epidemic predictions[J]. Med Rxiv.
- 16. (2020) . National Health Commission of the People’s Republic of China.http://www.nhc.gov.cn/yzygj/s7652m/202001/7450028ab6084101ae8110f0aaf81271.shtml[Accessed 08 .
- 17. (2020) . National Health Commission of the People’s Republic of China.http://www.nhc.gov.cn/yzygj/s7652m/202002/e84bd30142ab4d8982326326e4db22ea.shtml[Accessed 08 .
- 19.Riley S, Fraser C, C A Donnelly. (2003) Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. 300(5627), 1961-1966.
- 20.Oliveira E M de, Oliveira F L C. (2018) Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. 144-776.
- 21.Chen P, Yuan H, Shu X. (2008) Forecasting crime using the arima model[C]//2008. Fifth International Conference on Fuzzy Systems and Knowledge Discovery. IEEE 5, 627-630.
- 22.Li X. (2013) Comparison and analysis between holt exponential smoothing and brown exponential smoothing used for freight turnover. forecasts[C]//2013 Third International Conference on Intelligent System Design and Engineering Applications 453-456.
- 23.HANSUN S.A New Approach of Brown’s Double Exponential Smoothing Method in Time Series Analysis[J]. , Balkan Journal of Electrical and Computer Engineering 4(2), 75-78.
- 24.Chadsuthi S, Modchang C, Lenbury Y. (2012) Modeling seasonal leptospirosis transmission and its association with rainfall and temperature in Thailand using time–series and ARIMAX analyses[J]. Asian Pacific journal of tropical medicine. 5(7), 539-546.
- 25.Ming W, Huang J, Zhang C J P. (2020) Breaking down of healthcare system: Mathematical modelling for controlling the novel coronavirus (COVID-19) outbreak in. , Wuhan, China[J]. bioRxiv
- 26.Chowell G, Castillo-Chavez C, P W Fenimore. (2004) Model parameters and outbreak control for SARS[J]. Emerging Infectious Diseases. 10(7), 1258.
- 27.Luo H, Ye F, Sun T. (2004) In vitro biochemical and thermodynamic characterization of nucleocapsid protein of SARS[J]. Biophysical chemistry. 112(1), 15-25.
- 28.Colizza V, Barrat A, Barthélemy M. (2007) Predictability and epidemic pathways in global outbreaks of infectious diseases: the SARS case study[J]. , BMC medicine 5(1), 34.
Cited by (86)
This article has been cited by 86 scholarly works according to:
Citing Articles:
General Letters in Mathematics (2024) OpenAlex
Viruses (2023) OpenAlex
AIP conference proceedings (2023) OpenAlex
Current Opinion in Environmental Science & Health (2022) OpenAlex
International Journal of Environmental Research and Public Health (2022) OpenAlex
International Journal of System Dynamics Applications (2022) OpenAlex
International Journal of System Dynamics Applications (2022) Crossref
Computational and Mathematical Methods (2022) OpenAlex
Computational and Mathematical Methods in Medicine (2022) OpenAlex
Fractal and Fractional (2022) OpenAlex
Elsevier eBooks (2022) OpenAlex
2022 IEEE 10th International Conference on Healthcare Informatics (ICHI) (2021) OpenAlex
Results in Physics (2021) OpenAlex
Alexandria Engineering Journal (2021) OpenAlex
Mathematical Biosciences & Engineering (2021) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2021) OpenAlex
Chaos Solitons & Fractals (2021) OpenAlex
Journal of Engineering Research (2021) OpenAlex
The European Journal of Health Economics (2021) OpenAlex
Algorithms for intelligent systems (2021) OpenAlex
(2021) Crossref
Interface Focus (2021) OpenAlex
Journal of Economic Policy Researches / İktisat Politikası Araştırmaları Dergisi (2021) OpenAlex
Axioms (2021) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2021) OpenAlex
Infectious Disease Modelling (2021) OpenAlex
Journal of Mathematics Mechanics and Computer Science (2021) OpenAlex
International Journal of Mathematical Sciences and Computing (2021) OpenAlex
Mathematical Methods in the Applied Sciences (2021) OpenAlex
Applied Intelligence (2021) OpenAlex
Mathematical engineering (2021) OpenAlex
Journal of Interdisciplinary Mathematics (2021) OpenAlex
Journal of Complexity in Health Sciences (2021) OpenAlex
Communications in Mathematical Biology and Neuroscience (2021) OpenAlex
Infectious Disease Modelling (2021) OpenAlex
SN Computer Science (2021) OpenAlex
International Journal of Systems Assurance Engineering and Management (2021) OpenAlex
Physica A Statistical Mechanics and its Applications (2021) OpenAlex
(2021) OpenAlex
Studies in systems, decision and control (2021) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2021) OpenAlex
Advances in Difference Equations (2021) OpenAlex
International journal of intelligent engineering and systems (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
Advances in Difference Equations (2020) OpenAlex
International Journal of Clinical Biostatistics and Biometrics (2020) OpenAlex
Diabetes & Metabolic Syndrome Clinical Research & Reviews (2020) OpenAlex
Equilibrium Quarterly Journal of Economics and Economic Policy (2020) OpenAlex
Ingénierie des systèmes d information (2020) OpenAlex
SSRN Electronic Journal (2020) OpenAlex
Biomechanics and Modeling in Mechanobiology (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
IEEE Journal of Biomedical and Health Informatics (2020) OpenAlex
Chaos Solitons & Fractals X (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
Results in Physics (2020) OpenAlex
Journal of Nepal Mathematical Society (2020) OpenAlex
Jurnal Matematika MANTIK (2020) OpenAlex
IEEE Access (2020) OpenAlex
Journal of Applied Mathematics and Computing (2020) OpenAlex
Prithvi Academic Journal (2020) OpenAlex
Journal of Biological Dynamics (2020) OpenAlex
Alexandria Engineering Journal (2020) OpenAlex
Results in Applied Mathematics (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
Results in Physics (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
medRxiv (Cold Spring Harbor Laboratory) (2020) OpenAlex
arXiv (Cornell University) (2020) OpenAlex
International Journal of Advanced Engineering Research and Applications (2020) OpenAlex
Chaos Solitons & Fractals (2020) OpenAlex
Results in Physics (2020) OpenAlex
IEEE Internet of Things Journal (2020) OpenAlex